Spider Solitaire - Plan Before Vacating

Intro

There is a saying that goes, "Just because you can, it doesn't mean that you should."
This can be applied to the game of Spider Solitaire: "Just because you can vacate a column, it doesn't mean that you should."

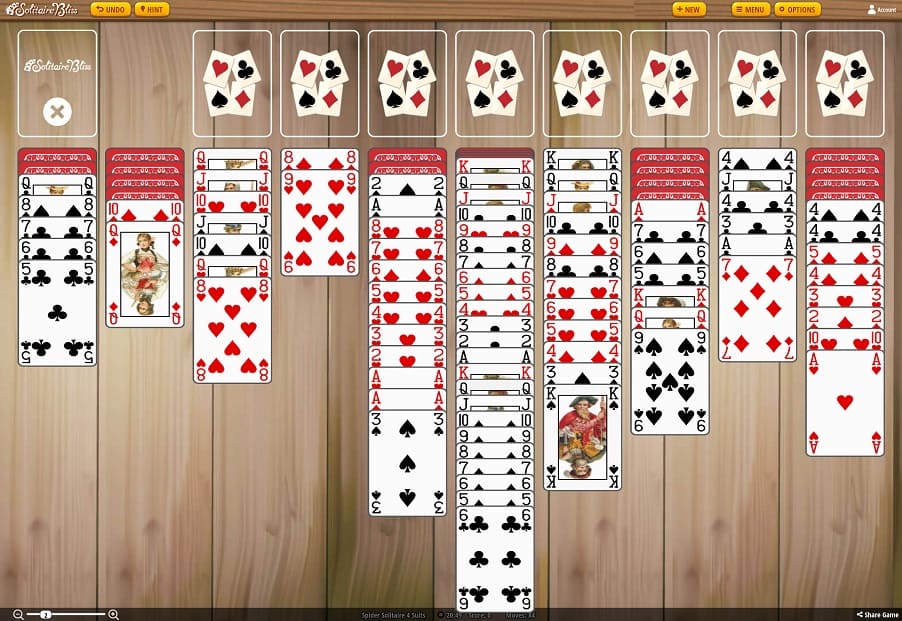
In figure 1 below is an actual pure game example. (No moves were undone.)

Game State

Figure 1 shows the state of a pure Spider Solitaire game immediately after the final deal.
As we can see, things weren't exactly going well. However, believe it or not, it's not a hopeless game.

The game state contains 20 hidden cards. This alone is enough to make winning difficult. No doubt it's the biggest problem. However, to make matters even worse, the game state also contains 23 breaks in ranks, numerous breaks in suit, and only 1 King has been extracted. There are 4 more Kings that need to be exacted, and somewhere in the hidden cards are the last 3.

Pile 6 is a nightmare. It contains 27 cards, 4 of which are hidden and 2 of which are Kings. The only good thing is that there are only 2 rank breaks. To reach the hidden cards, other than removing the Six from the bottom, both Kings will need to be extracted.
It's not likely to be easy.

The good news is that the game state contains several good runs, even if they do contain many suit breaks. As well, it's very apparent that column 4 could be vacated in as little as 3 moves.
The question is, what then?

Obstacles vs. Resources

Reaching a game state such as shown in figure 1 is not at all unusual for me. Many I win, and many I lose.
In this case, at first, I estimated my chances to be very low, but after analyzing the game state thoroughly, I estimated my chances at perhaps 1 in 3.
However, that might have been a bit optimistic.

In any event, as is very often the case, the deciding factor was going to be the order in which the hidden cards were to turn.
If the wrong card were to turn at the wrong time, the game would be over.

In the game state, it can be seen that there are 23 rank breaks. Most players see these as obstacles that must be overcome in order to win. While this is very true, I find that it helps to see the 17 non-ace rank breaks as resources.
As well, the 9 non-ace open (bottom) cards are also resources. This makes a total of 26 resource cards. (A vacant column is also a resource, a very important one.)

For example, the Ten of diamonds in pile 2 is a resource card because it doesn't have a Nine (of any suit) atop of it.

If the Queen were removed from atop of the Ten, a nine-headed run could be placed there. The Ten of diamonds would then be overcome (often called used) and no longer a resource.
The aforementioned resource cards all represent opportunities. The question is, can the resources be exploited in a manner that will win the game? Of course, the process is greatly compounded by having to maneuver around suit breaks. (A suit break is a change of suit within a run.)

The Plan

In the game state seen in figure 1, the most obvious plan would be to move the Queen from pile 2 onto the King in pile 7, then the Nine and Eight in pile 4 could be placed onto the newly opened Ten of diamonds. Column 4 would then be empty, which would give the game state some mobility.
So far so good. Now what? Having a plan isn't enough if there's no more beneficial play.

By making use of the vacant column for temporary storage, the Eight-Five run could be moved from pile 1 onto the Nine in pile 7. Then, the Queen could be moved from pile 1 into the vacant column, which would turn a hidden card in pile 1.

Looking at the other piles, it would seem that no other pile could be turned (meaning to turn a hidden card). Therefore, there would seem to be no other option than to turn pile 1 and hope for the best.
If both of the hidden cards could be placed, then what? It depends on what turns up and how it affects the present resources. The best scenario would be if two columns were left empty. We can't count of this, but it's possible. If only one column is left empty, it could be the end of the game.

If a two were to turn, it looks like column 9 could easily be emptied; that is, unless the first turn messed it up. The odds of winning don't appear to be very good. But, we have our plan, to vacate column 4 and use it to turn pile 1.

Better Plan?

The original plan to turn pile 1 stood a rather poor chance of leading to a victory. However, there was a way to improve the odds a little bit, so I took it.

The reason I modified the plan was that, after losing very many games, I finally learned to keep as many options open for as long as possible. In a case like this one, it might seem that it wouldn't make a real difference, but it often does, and it did in this case.

From figure 1, it's easy to see that pile 1 could be turned in just 3 moves, without the need to vacate a column. That was the simple plan that I followed. Of course, I also had my eye on pile 9 because, if a Two was to turn in pile 1, I was planning on emptying column 9. And if a Two failed to turn, as long as I had a vacant column, I'd likely still be able to vacate column 9, which would leave new opportunities, but probably only one vacant column.

The drawback of my new plan was that the King in pile 7 would be filled with the Queen from pile 1, as opposed to going into a vacant column. This meant that the Queen in pile 2 would have to stay put. What this meant was, unless a King turned in pile 1, pile 4 could not be vacated. If column 1 did not clear, and both a King and a Two failed to turn, the game would be over very quickly.

The advantage of my new plan was that, after turning the first hidden card in pile 1, there would still be an open Nine, in pile 4. This was not the case for the original plan. This simple fact would improve my chances of vacating column 1 a little bit. There were 7 visible Eights, which would mean perhaps a 1 in 13 chance on an Eight turning in pile 1.

I put my new plan into action. The Five of spades and the Eight of diamonds were under the Queen of clubs in pile 1. If I'd have stuck with the original plan, the game would have been a loss. I was able to vacate pile 1, which gave me a fighting chance.

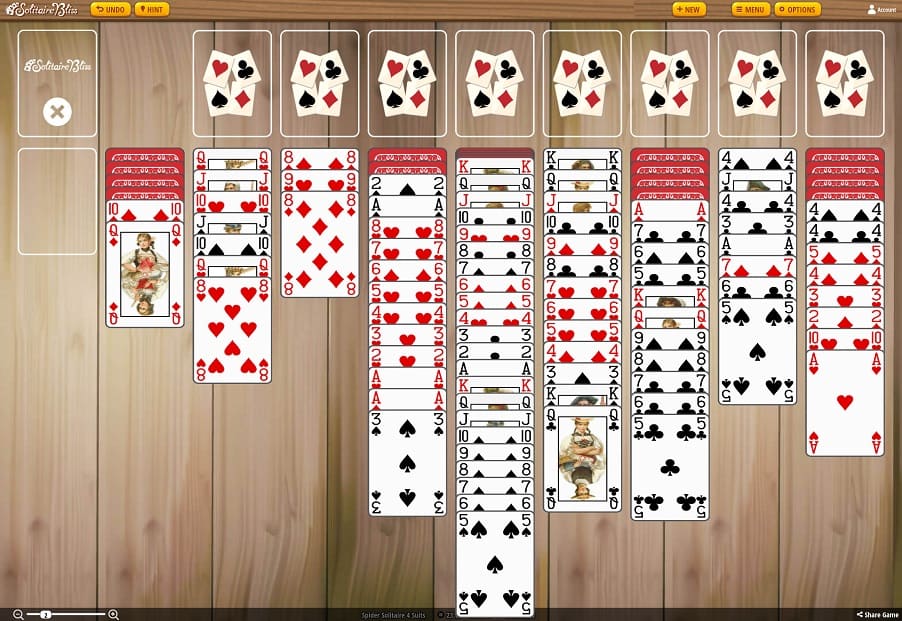
The Play

I was hoping for a Two to turn. With 4 Twos somewhere in the 20 hidden cards, and possibly two chances at getting one, I knew that my chances were quite good. I also knew that a King would allow me to vacate pile 4. As can be seen in figure 1, there were 3 hidden Kings.

I could have also handled a Four, Five, Six, Seven, Eight, or Jack. Depending on the first turn, it would change what second turn I could place. In reality, my chances of vacating pile 1 were probably much better than one might think.

The first card to turn in pile 1 was the Five of spades. It was not the Two I was hoping for, but I figured it might come out on the second turn. Next came the Eight of diamonds, which I promptly plopped onto pile 4, leaving column 1 vacate. The result is shown in figure 2.

To make a long story short, I then vacated pile 9, which left the Ace of clubs in column 1. Next, I performed as much reordering as I could, turned the 4 hidden cards in pile 2, reordered again, build hearts, build spades, and reordered again.

After that, things were so well ordered that no matter what was to turn was going to be placed. Victory wasn't overly difficult, and without ever undoing a move.

The point of this exercise is that just because a column can easily be vacated, it's not always the best way to begin a plan.

Addendum

In figure 3 can be seen the game state after I turned the cards from pile 2 and performed some reordering. At this point, after analyzing the game state and devising a plan, I feel that my chances of winning were now well in my favor. However, I also knew that it wasn't a sure thing and that I needed to be very careful.

In my inexperienced days, my next move would have been to simply move the King-Five run of diamonds from pile 6 into the vacant column. This would have been a gigantic mistake.

Instead, I turned pile 5. Even if the column had not been vacated, I still would have had a vacant column and would have been able to then turn pile 6. As it turned out, column 5 did vacate, which left me with two empty columns. Even with 12 hidden cards to go, it was an easy win from there on in.

Everything that's needed to devise the plan can be seen in figure 3. Since it's good practice for a learning player to visualize plans, I'll leave it as an exercise.

In my case, from the game state in figure 3, it took me 59 moves to turn pile 5. A lot of the moves were reordering that don't really need to be visualized, as long as the player knows what can and cannot be ordered.

For anyone who believes that opportunities for plans like this are rare, I can tell you that they're not. In this case, I had to set up the plan, which took several moves. Certain cards had to be just in the right place. It was not as easy to spot the plan before then. But still, it was there waiting for me.

As a clue, the first move of the plan was to extract the King from pile 7. From there, there was no doubt in my mind that I'd be turning pile 5, and that column 9 would be left empty.